Les matrices et les transformations

Introduction

Avant de lire ce tutoriel, nous vous recommandons de lire attentivement et de comprendre le tutoriel Mathématiques des vecteurs, car ce tutoriel nécessite une connaissance des vecteurs.

Ce tutoriel traite des transformations et de la façon dont nous les représentons dans Godot à l'aide de matrices. Il ne s'agit pas d'un guide complet et approfondi sur les matrices. Les transformations sont la plupart du temps appliquées sous forme de translation, de rotation et de mise à l'échelle. Nous nous concentrerons donc sur la façon de représenter celles-ci à l'aide de matrices.

La majeure partie de ce guide se concentre sur la 2D, en utilisant Transform2D et Vector2, mais la façon dont les choses fonctionnent en 3D est très similaire.

Note

Comme mentionné dans le précédent tutoriel, il est important de se rappeler que dans Godot, l'axe Y pointe vers le bas en 2D. C'est le contraire de la façon dont la plupart des écoles enseignent l'algèbre linéaire, avec l'axe Y pointant vers le haut.

Note

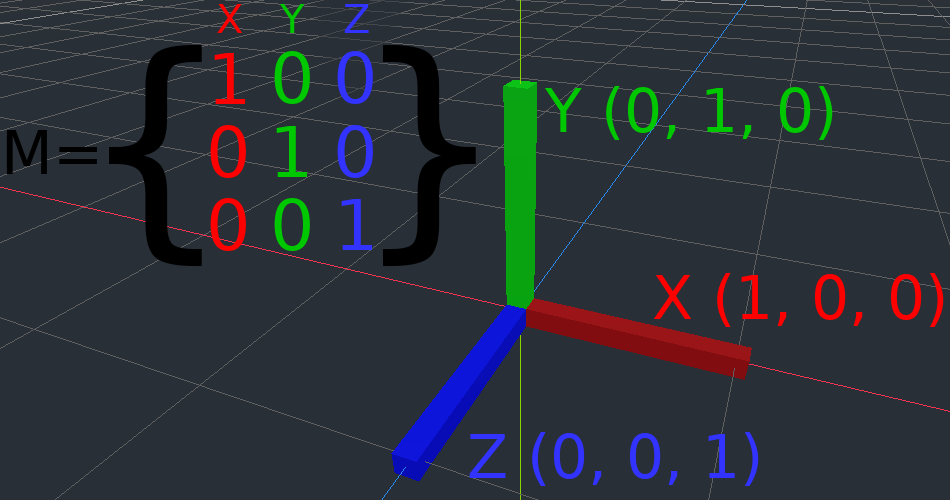
La convention est que l'axe X est rouge, l'axe Y est vert et l'axe Z est bleu. Ce tutoriel est codé par couleur pour correspondre à ces conventions, mais nous allons également représenter le vecteur d'origine avec une couleur bleue.

Composantes de la matrice et matrice d'identité

La matrice d'identité représente une transformation sans translation, sans rotation et sans mise à échelle. Commençons par regarder la matrice d'identité et comment ses composants sont liés à la façon dont elle apparaît visuellement.

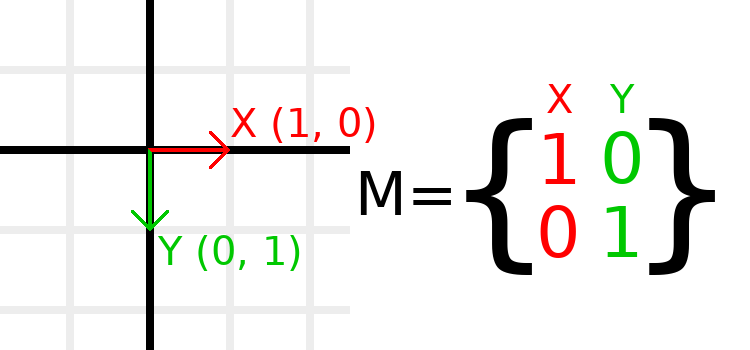
Les matrices ont des lignes et des colonnes, et une matrice de transformation a des conventions spécifiques sur ce que chacune fait.

Dans l'image ci-dessus, nous pouvons voir que le vecteur X rouge est représenté par la première colonne de la matrice, et le vecteur Y vert est également représenté par la deuxième colonne. Une modification des colonnes modifiera ces vecteurs. Nous verrons comment ils peuvent être manipulés dans les quelques exemples suivants.

Vous ne devez pas vous soucier de manipuler directement les lignes, car nous travaillons généralement avec les colonnes. Cependant, vous pouvez considérer les lignes de la matrice comme montrant quels vecteurs contribuent au déplacement dans une direction donnée.

Lorsque nous faisons référence à une valeur telle que t.x.y, c'est la composante Y du vecteur de la colonne X. En d'autres termes, la partie inférieure gauche de la matrice. De même, t.x.x est en haut à gauche, t.y.x est en haut à droite, et t.y.y est en bas à droite, où t est la Transform2D.

Mise à l'échelle de la matrice de transformation

L'application d'une mise à l'échelle est l'une des opérations les plus faciles à comprendre. Commençons par placer le logo Godot sous nos vecteurs afin de pouvoir voir visuellement les effets sur un objet :

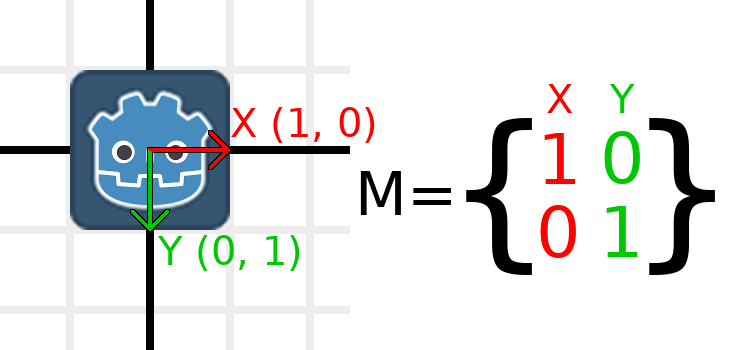
Maintenant, pour mettre la matrice à l'échelle, il suffit de multiplier chaque élément par l'échelle que nous voulons. Augmentons l'échelle de 2. 1 fois 2 devient 2, et 0 fois 2 devient 0, donc nous obtenons ceci :

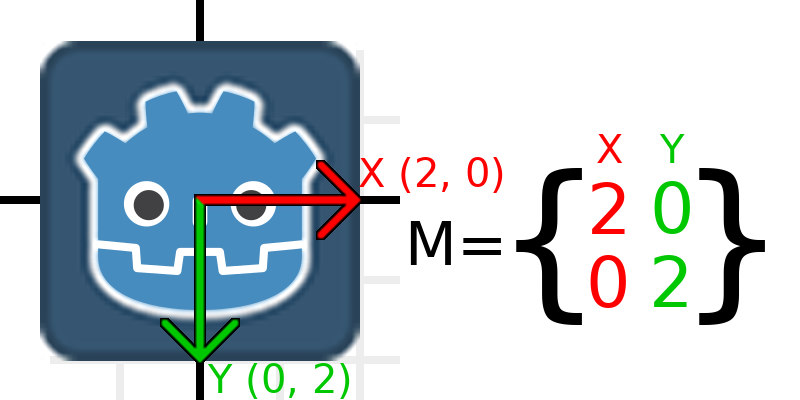
Pour faire cela en code, on peut simplement multiplier chacun des vecteurs :

GDScriptC#

var t = Transform2D()
# Scale
t.x *= 2
t.y *= 2
transform = t # Change the node's transform to what we just calculated.

Si nous voulions le ramener à son échelle initiale, nous pourrions multiplier chaque composante par 0,5. C'est à peu près tout ce qu'il y a à savoir pour mettre à l'échelle une matrice de transformation.

Pour calculer l'échelle de l'objet à partir d'une matrice de transformation existante, vous pouvez utiliser length() sur chacun des vecteurs de colonne.

Note

Dans les projets réels, vous pouvez utiliser la méthode scaled() pour effectuer une mise à l'échelle.

Rotation de la matrice de transformation

Nous allons commencer de la même manière que précédemment, avec le logo Godot sous la matrice d'identité :

A titre d'exemple, disons que nous voulons faire pivoter notre logo Godot de 90 degrés dans le sens des aiguilles d'une montre. À l'heure actuelle, l'axe X pointe vers la droite et l'axe Y pointe vers le bas. Si nous les faisons pivoter dans notre tête, nous verrons logiquement que le nouvel axe X devrait pointer vers le bas et le nouvel axe Y vers la gauche.

Vous pouvez imaginer que vous saisissez à la fois le logo Godot et ses vecteurs, puis les tourner autour du centre. Où que vous finissiez la rotation, l'orientation des vecteurs détermine ce qu'est la matrice.

Nous devons représenter "en bas" et "à gauche" en coordonnées normales, ce qui signifie que nous allons mettre X à (0, 1) et Y à (-1, 0). Ce sont également les valeurs de Vector2.DOWN et Vector2.LEFT. Lorsque nous faisons cela, nous obtenons le résultat souhaité de la rotation de l'objet :

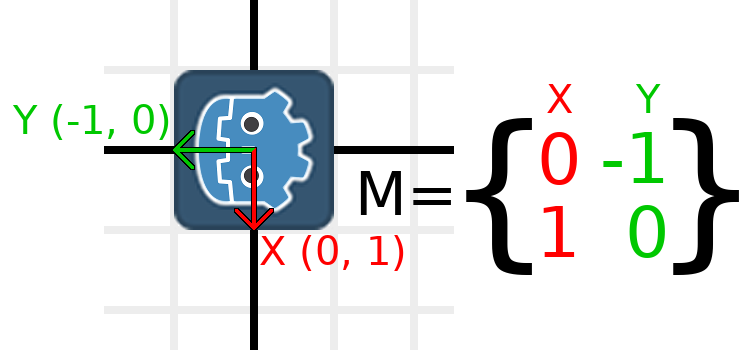
Si vous avez du mal à comprendre ce qui précède, essayez cet exercice : Coupez un carré de papier, tracez des vecteurs X et Y par-dessus, placez-le sur du papier millimétré, puis faites-le tourner et notez les points d'extrémité.

Pour effectuer une rotation en code, nous devons pouvoir calculer les valeurs via le programme. Cette image montre les formules nécessaires pour calculer la matrice de transformation à partir d'un angle de rotation. Ne vous inquiétez pas si cette partie vous semble compliquée, je vous promets que c'est la chose la plus difficile à savoir.

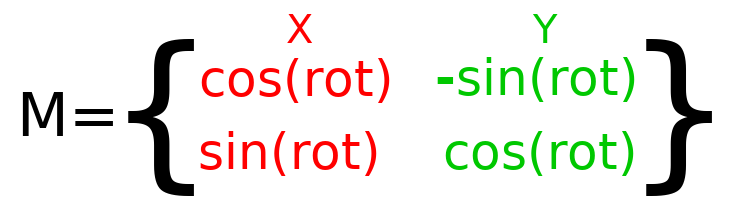
Note

Godot représente toutes les rotations avec des radians, pas des degrés. Un tour complet est en radians TAU ou PI*2, et un quart de tour de 90 degrés est en radians TAU/4 ou PI/2. Travailler avec TAU permet généralement d'obtenir un code plus lisible.

Note

Fait amusant : en plus du fait que Y soit en bas dans Godot, la rotation est représentée dans le sens des aiguilles d'une montre. Cela signifie que toutes les fonctions mathématiques et de trigonométrie se comportent de la même manière qu'un système CCW Y-is-up (Y est en haut), puisque ces différences "s'annulent". Vous pouvez penser que les rotations dans les deux systèmes sont "de X à Y".

Afin d'effectuer une rotation de 0,5 radians (environ 28,65 degrés), nous ajoutons simplement une valeur de 0,5 à la formule ci-dessus et évaluons pour trouver quelles devraient être les valeurs réelles :

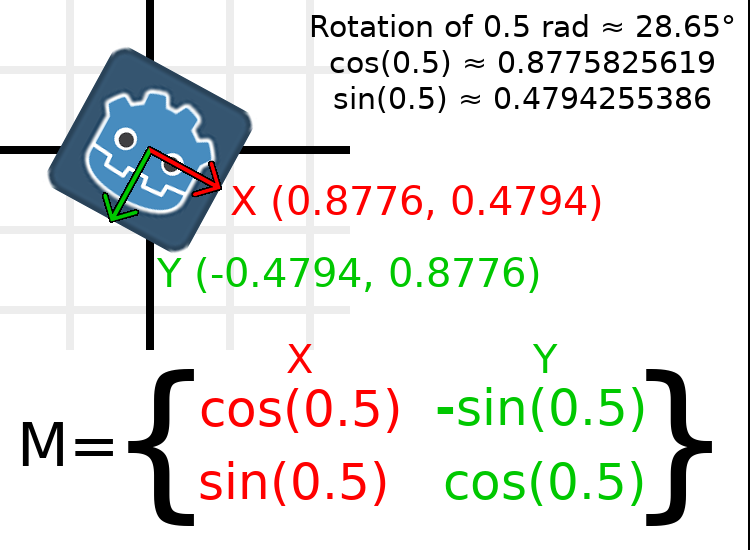
Voici comment cela serait fait en code (placer le script sur un Node2D) :

GDScriptC#

var rot = 0.5 # The rotation to apply.
var t = Transform2D()
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
transform = t # Change the node's transform to what we just calculated.

Pour calculer la rotation de l'objet à partir d'une matrice de transformation existante, vous pouvez utiliser atan2(t.x.y, t.x.x), où t est le Transform2D.

Note

Dans les projets réels, vous pouvez utiliser la méthode rotated() pour effectuer des rotations.

Base de la matrice de transformation

Jusqu'à présent, nous n'avons travaillé qu'avec les vecteurs x et y, qui sont chargés de représenter la rotation, la mise à l'échelle et/ou le cisaillement (avancé, couvert à la fin). Les vecteurs X et Y sont appelés ensemble la base de la matrice de transformation. Il est important de connaître les termes "base" et "vecteurs de base".

Vous avez peut-être remarqué que Transform2D a en fait trois valeurs Vector2 : x, y, et origine. La valeur origin ne fait pas partie de la base, mais elle fait partie de la transformation, et nous en avons besoin pour représenter la position. A partir de maintenant, nous allons suivre le vecteur d'origine dans tous les exemples. Vous pouvez considérer l'origine comme une autre colonne, mais il est souvent préférable de la considérer comme complètement séparée.

Notez qu'en 3D, Godot a une structure Basis séparée pour contenir les trois valeurs Vector3 de la base, car le code peut devenir complexe et il est logique de la séparer de Transform (qui est composé d'une Basis et d'une Vector3 supplémentaire pour l'origine).

Translation de la matrice de transformation

La modification du vecteur origin est appelée une translation de la matrice de transformation. La translation est essentiellement un terme technique pour "déplacer" l'objet, mais elle n'implique explicitement aucune rotation.

Travaillons à travers un exemple pour aider à comprendre cela. Nous commencerons par la transformation d'identité comme la dernière fois, sauf que nous allons suivre le vecteur d’origine cette fois.

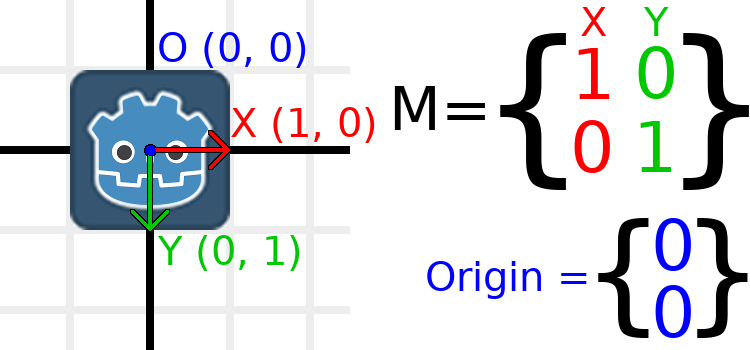
Si nous voulons que l'objet se déplace vers une position de (1, 2), nous devons simplement mettre son vecteur origin à (1, 2) :

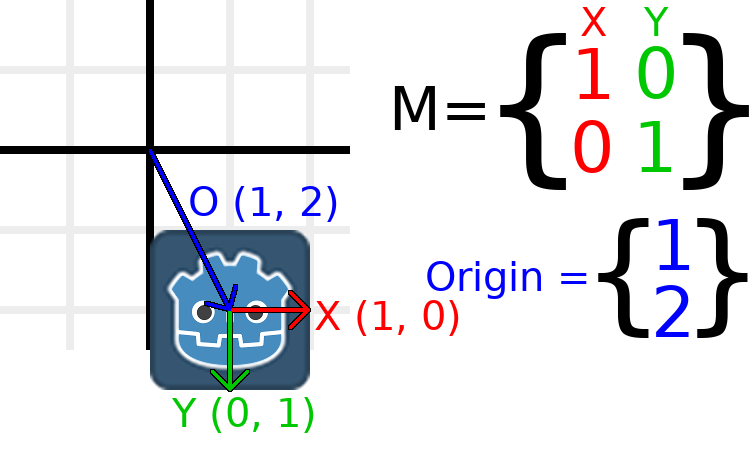
Il existe également une méthode translated(), qui effectue une opération différente pour ajouter ou modifier directement origine. La méthode translated() translaera l'objet par rapport à sa propre rotation. Par exemple, un objet tourné de 90 degrés dans le sens des aiguilles d'une montre se déplacera vers la droite lorsqu'il sera translated() avec Vector2.UP.

Note

La 2D de Godot utilise des coordonnées basées sur les pixels, donc dans les projets réels, vous voudrez translater par des centaines d'unités.

Mettre tout cela ensemble

Nous allons appliquer tout ce que nous avons mentionné jusqu'à présent à une transformation. Pour suivre, ouvrez-vous un projet simple avec un nœud Sprite et utiliser le logo Godot comme ressource de texture.

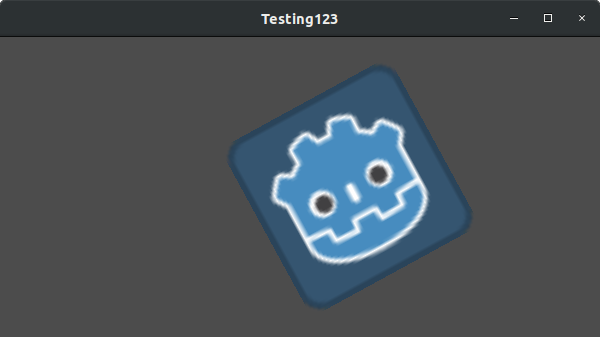
Mettons la translation à (350, 150), une rotation de -0,5 rad, et une échelle de 3. J'ai posté une capture d'écran, et le code pour la reproduire, mais je vous encourage à essayer de reproduire la capture d'écran sans regarder le code !

GDScriptC#

var t = Transform2D()
# Translation
t.origin = Vector2(350, 150)
# Rotation
var rot = -0.5 # The rotation to apply.
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
# Scale
t.x *= 3
t.y *= 3
transform = t # Change the node's transform to what we just calculated.

Cisaillement de la matrice de transformation (avancé)

Note

Si vous cherchez seulement à savoir comment utiliser les matrices de transformation, n'hésitez pas à sauter cette section du tutoriel. Cette section explore un aspect peu utilisé des matrices de transformation dans le but d'en faciliter la compréhension.

Vous avez peut-être remarqué qu'une transformation a plus de degrés de liberté que la combinaison des actions ci-dessus. La base d'une matrice de transformation 2D a quatre nombres totaux en deux valeurs Vector2, alors qu'une valeur de rotation et un Vector2 pour l'échelle n'ont que 3 nombres. Le concept de haut niveau pour le degré de liberté manquant est appelé cisaillement.

Normalement, les vecteurs de base seront toujours perpendiculaires entre eux. Cependant, le cisaillement peut être utile dans certaines situations, et comprendre le cisaillement vous aide à comprendre comment fonctionnent les transformations.

Pour vous montrer visuellement ce à quoi il ressemblera, superposons une grille au logo Godot :

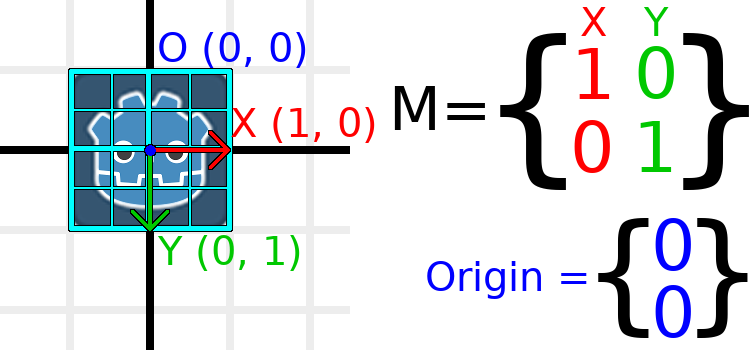
Chaque point de cette grille est obtenu en additionnant les vecteurs de base. Le coin inférieur droit est X + Y, tandis que le coin supérieur droit est X - Y. Si nous changeons les vecteurs de base, toute la grille se déplace avec, car la grille est composée des vecteurs de base. Toutes les lignes de la grille qui sont actuellement parallèles le resteront, quelles que soient les modifications que nous apportons aux vecteurs de base.

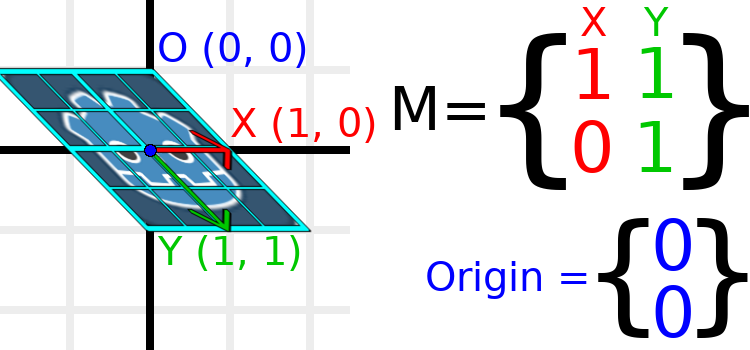
À titre d'exemple, mettons Y à (1, 1) :

GDScriptC#

var t = Transform2D()
# Shear by setting Y to (1, 1)
t.y = Vector2.ONE
transform = t # Change the node's transform to what we just calculated.

Note

Vous ne pouvez pas définir les valeurs brutes d'un Transform2D dans l'éditeur, donc vous devez utiliser du code si vous voulez cisailler l'objet.

Les vecteurs n'étant plus perpendiculaires, l'objet a été cisaillé. Le centre inférieur de la grille, qui est (0, 1) par rapport à lui-même, est maintenant situé à une position mondiale de (1, 1).

Les coordonnées intra-objet sont appelées coordonnées UV dans les textures, alors empruntons cette terminologie pour ici. Pour trouver la position mondiale à partir d'une position relative, la formule est U * X + V * Y, où U et V sont des nombres et X et Y sont les vecteurs de base.

Le coin inférieur droit de la grille, qui est toujours à la position UV de (1, 1), est à la position mondiale de (2, 1), qui est calculée à partir de X*1 + Y*1, qui est (1, 0) + (1, 1), ou (1 + 1, 0 + 1), ou (2, 1). Cela correspond à notre observation de l'endroit où se trouve le coin inférieur droit de l'image.

De même, le coin supérieur droit de la grille, qui est toujours à la position UV de (1, -1), est à la position mondiale de (0, -1), qui est calculée à partir de X*1 + Y*-1, qui est (1, 0) - (1, 1), ou (1 - 1, 0 - 1), ou (0, -1). Cela correspond à notre observation de l'endroit où se trouve le coin supérieur droit de l'image.

Nous espérons que vous comprenez maintenant parfaitement comment une matrice de transformation affecte l'objet, et la relation entre les vecteurs de base et comment les "UV" ou "intra-coordonnées" de l'objet ont changé leur position dans le monde.

Note

Dans Godot, toutes les transformations mathématiques sont effectuées par rapport au nœud parent. Lorsque nous parlons de "position mondiale", ce serait plutôt par rapport au parent du nœud, si le nœud avait un parent.

Si vous souhaitez des explications supplémentaires, vous pouvez consulter l'excellente vidéo de 3Blue1Brown sur les transformations linéaires : https://www.youtube.com/watch?v=kYB8IZa5AuE

Applications pratiques des transformations

Dans les projets réels, vous travaillerez généralement avec des transformations à l'intérieur de transformations en ayant plusieurs nœuds Node2D ou Spatial parentés les uns aux autres.

Cependant, il est parfois très utile de calculer manuellement les valeurs dont nous avons besoin. Nous allons voir comment vous pouvez utiliser Transform2D ou Transform pour calculer manuellement les transformations des nœuds.

Convertir les positions entre les transformations

Il y a de nombreux cas où vous voudriez convertir une position dans et hors d'une transformation. Par exemple, si vous avez une position relative au joueur et que vous souhaitez trouver la position mondiale (par rapport au parent), ou si vous avez une position mondiale et que vous souhaitez savoir où elle se trouve par rapport au joueur.

On peut trouver ce qu'un vecteur relatif au joueur serait défini dans l'espace mondial en utilisant la méthode "xform" :

GDScriptC#

# World space vector 100 units below the player.
print(transform.xform(Vector2(0, 100)))

Et nous pouvons utiliser la méthode "xform_inv" pour trouver quelle serait la position spatiale mondiale si elle était plutôt définie par rapport au joueur :

GDScriptC#

# Where is (0, 100) relative to the player?
print(transform.xform_inv(Vector2(0, 100)))

Note

Si vous savez à l'avance que la transformation est positionnée à (0, 0), vous pouvez utiliser les méthodes "basis_xform" ou "basis_xform_inv" à la place, qui permettent d'éviter de traiter la translation.

Déplacement d'un objet par rapport à lui-même

Une opération courante, en particulier dans les jeux en 3D, consiste à déplacer un objet par rapport à lui-même. Par exemple, dans les jeux de tir à la première personne, vous voudriez que le personnage se déplace vers l'avant (axe -Z) lorsque vous appuyez sur W.

Puisque les vecteurs de base sont l'orientation par rapport au parent, et que le vecteur d'origine est la position par rapport au parent, nous pouvons simplement ajouter des multiples des vecteurs de base pour déplacer un objet par rapport à lui-même.

Ce code permet de déplacer un objet de 100 unités à sa propre droite :

GDScriptC#

transform.origin += transform.x * 100

Pour se déplacer en 3D, il faudrait remplacer "x" par "basis.x".

Note

Dans les projets réels, vous pouvez utiliser translate_object_local en 3D ou move_local_x et move_local_y en 2D pour le faire.

Application de transformations sur des transformations

L'une des choses les plus importantes à savoir sur les transformations est la façon dont vous pouvez en utiliser plusieurs ensemble. La transformation d'un nœud parent affecte tous ses enfants. Disséquons un exemple.

Dans cette image, le nœud enfant a un "2" après les noms des composants pour les distinguer du nœud parent. Cela peut sembler un peu écrasant avec autant de chiffres, mais souvenez-vous que chaque chiffre est affiché deux fois (à côté des flèches et également dans les matrices), et que près de la moitié des chiffres sont des zéros.

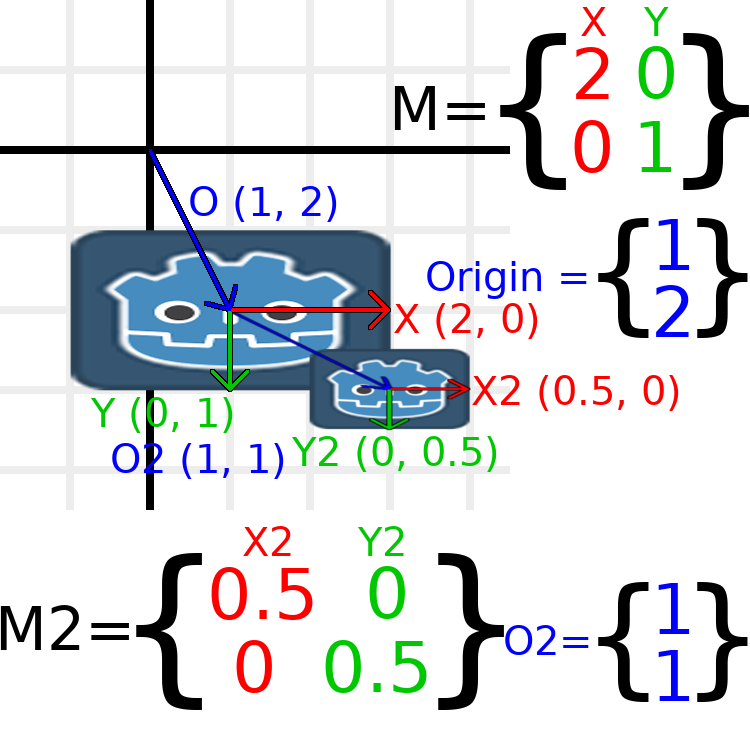
Les seules transformations en cours ici sont que le nœud parent a reçu une échelle de (2, 1), l'enfant a reçu une échelle de (0,5, 0,5) et les deux nœuds ont reçu des positions.

Toutes les transformations des enfants sont affectées par les transformations des parents. L'enfant a une échelle de (0,5, 0,5), on s'attendrait donc à ce que ce soit un carré de rapport 1:1, et c'est le cas, mais seulement par rapport au parent. Le vecteur X de l'enfant finit par être (1, 0) dans l'espace mondial, car il est mis à l'échelle par les vecteurs de base du parent. De même, le vecteur origin du nœud enfant est fixé à (1, 1), mais il est en fait déplacé (2, 1) dans l'espace mondial, en raison des vecteurs de base du nœud parent.

Pour calculer manuellement la transformation de l'espace mondial d'un enfant, c'est le code que nous utiliserions :

GDScriptC#

# Set up transforms just like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))

# Calculate the child's world space transform
# origin = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
var origin = parent.x * child.origin.x + parent.y * child.origin.y + parent.origin
# basis_x = (2, 0) * 0.5 + (0, 1) * 0
var basis_x = parent.x * child.x.x + parent.y * child.x.y
# basis_y = (2, 0) * 0 + (0, 1) * 0.5
var basis_y = parent.x * child.y.x + parent.y * child.y.y

# Change the node's transform to what we just calculated.
transform = Transform2D(basis_x, basis_y, origin)

Dans les projets actuels, nous pouvons trouver la transformation mondiale de l'enfant en appliquant une transformation sur une autre en utilisant l'opérateur * :

GDScriptC#

# Set up transforms just like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))

# Change the node's transform to what would be the child's world transform.
transform = parent * child

Note

Quand on multiplie des matrices, l'ordre compte ! Ne les mélangez pas.

Enfin, appliquer la transformation d'identité ne fera rien.

Si vous souhaitez des explications supplémentaires, vous pouvez consulter l'excellente vidéo de 3Blue1Brown sur la composition des matrices : https://www.youtube.com/watch?v=XkY2DOUCWMU

Inverser une matrice de transformation

La fonction "affine_inverse" renvoie une transformation qui "annule" la transformation précédente. Cette fonction peut être utile dans certaines situations, mais il est plus facile de se contenter de quelques exemples.

La multiplication d'une transformation inverse par la transformation normale annule toutes les transformations :

GDScriptC#

var ti = transform.affine_inverse()
var t = ti * transform
# The transform is the identity transform.

La transformation d'une position par une transformation et son inverse aboutit à la même position (idem pour "xform_inv") :

GDScriptC#

var ti = transform.affine_inverse()
position = transform.xform(position)
position = ti.xform(position)
# The position is the same as before.

Comment tout cela fonctionne-t-il en 3D ?

L'un des grands avantages des matrices de transformation est qu'elles fonctionnent de manière très similaire entre les transformations 2D et 3D. Tout le code et les formules utilisés ci-dessus pour la 2D fonctionnent de la même façon en 3D, à trois exceptions près : l'ajout d'un troisième axe, que chaque axe est du type Vector3, et aussi que Godot stocke la Basis séparément de la Transform, puisque les mathématiques peuvent devenir complexe et qu'il est logique de la séparer.

Tous les concepts relatifs au fonctionnement de la translation, de la rotation, de l'échelle et du cisaillement en 3D sont les mêmes qu'en 2D. Pour l'échelle, nous prenons chaque composante et la multiplions ; pour la rotation, nous modifions l'endroit où chaque vecteur de base pointe ; pour la translation, nous manipulons l'origine ; et pour le cisaillement, nous modifions les vecteurs de base pour qu'ils soient non-perpendiculaires.

Si vous le souhaitez, il est bon de jouer avec les transformations pour comprendre leur fonctionnement. Godot vous permet d'éditer des matrices de transformation 3D directement depuis l'inspecteur. Vous pouvez télécharger ce projet qui comporte des lignes et des cubes colorés pour vous aider à visualiser les vecteurs Basis et l'origine en 2D et 3D : https://github.com/godotengine/godot-demo-projects/tree/master/misc/matrix_transform

Note

La section "Matrix" de Spatial dans l'inspecteur de Godot 3.2 affiche la matrice telle qu'elle a été transposée, avec les colonnes horizontales et les lignes verticales. Cela pourrait être modifié pour être moins déroutant dans une prochaine version de Godot.

Note

Vous ne pouvez pas modifier la matrice de transformation de Node2D directement dans l'inspecteur de Godot 3.2. Cela pourrait être modifié dans une future version de Godot.

Si vous souhaitez des explications supplémentaires, vous pouvez consulter l'excellente vidéo de 3Blue1Brown sur les transformations linéaires en 3D : https://www.youtube.com/watch?v=rHLEWRxRGiM

Représentation de la rotation en 3D (avancé)

La plus grande différence entre les matrices de transformation 2D et 3D est la façon dont vous représentez la rotation par elle-même sans les vecteurs de base.

Avec la 2D, nous avons un moyen facile (atan2) de passer d'une matrice de transformation à un angle. En 3D, nous ne pouvons pas simplement représenter la rotation comme un seul chiffre. Il existe quelque chose appelé angles d'Euler, qui peut représenter les rotations comme un ensemble de 3 nombres, mais ils sont limités et peu utiles, sauf dans des cas triviaux.

En 3D, nous n'utilisons généralement pas d'angles, nous utilisons soit une base de transformation (utilisée à peu près partout dans Godot), soit des quaternions. Godot peut représenter les quaternions en utilisant la structure Quat. Je vous suggère d'ignorer complètement comment ils fonctionnent sous le capot, car ils sont très compliqués et peu intuitifs.

Cependant, si vous voulez vraiment savoir comment cela fonctionne, voici quelques ressources intéressantes, que vous pouvez suivre dans l'ordre :

https://www.youtube.com/watch?v=mvmuCPvRoWQ

https://www.youtube.com/watch?v=d4EgbgTm0Bg

https://eater.net/quaternions